 terabo.net
terabo.net 人生ラボラボ
宇宙一馬鹿げたルービックキューブの解き方
去年の記事「ルービックキューブをアルゴリズムで解くということ」に続き,ルービックキューブとアルゴリズム ネタシリーズ第2弾です.
今回は宇宙一無駄な努力をしてルービックキューブを解く方法です.
無駄な努力
スピードキューバ(ルービックキューブを早く解くことを追求する人たち)には常識的に知られていることですが,ルービックキューブは容易に分解できます.

したがって,未完成状態のルービックキューブを分解して,物理的に組み上げることでルービックキューブを完成させることができます.
この一連の操作を目をつぶった状態で実行するとどうでしょうか.
それは多分一生完成しないだろうと予想されるでしょう.全くその通りです.
この手法は言い換えると次のようになります.
アルゴリズムBG:
入力: スクランブルされたキューブ
出力: 完成状態のキューブ
(Step 1) ルービックキューブのパーツを分解する.
(Step 2) 分解したパーツをシャッフルする.
(Step 3) シャッフルされた順にキューブを組み上げていく.
(Step 4) キューブが完成したら終了,完成しない場合 Step 1 に戻る.
コンピュータサイエンスを(ネタ的に)知っている人ならピンとくると思います,これはボゴソートに対応します.
ボゴソート (英語: bogosort) は、ソートのアルゴリズムの一つ。平均的な計算時間はO(n×n!)で、非常に効率の悪いアルゴリズムとして知られている。安定ソートではない。 ボゴソート – Wikipedia より
こんなの終わるわけないやんと思いますが,「無限の猿の定理」により十分長い時間をかければ完成することは示せます.
完成までの試行回数(キューブが組み上げられた回数は)は平均で $ T_{bg} = (8! \cdot 3^{8} \cdot 12! \cdot 2^{12}) / 2 = 259512019646939136000 $ 回です.
これはエッジの位置と向き,コーナーの位置と向きの全パターンの半分です.
平均がなぜ半分でいいのかよくわかりませんが,以下の文献でそう書いてあったので半分にしてます.
参考文献: Bogobogosortについて – w125のブログ
さて,1回キューブを組み立てるのに1分要すると仮定します.
すると完成するのに 259512019646939136000分 かかる計算になります.これは,493744329617464年,すなわち 493兆7443億年です.
ちなみに地球が誕生したのは46億年前,宇宙が生成されたのが138億年前とされています.
以下の文献により,「無限の猿定理」で最も例に取り上げられる,1秒間に10万文字タイプできる猿がハムレットを執筆するのに $ 10^{360790.5} $ 年要するとされていますので,ハムレットを書くのとルービックキューブを揃えるのは確率的にはルービックキューブを揃える方がずっとずっと簡単なのです.
参考文献: 時間の比較 – ニコニコ動画:GINZA http://www.nicovideo.jp/watch/nm16202721
最良で1回の試行回数で完成しますが,この確率は限りなく0に近です.最悪の場合の試行回数は無限大です.
めげない努力
一旦ばらばらに分解してから組み上げるのはさすがに馬鹿すぎるでしょう.
ちゃんとルービックキューブのパズルらしく面を回転させて完成させます.
しかし,回転させるといってもどの面をどの向きに回転させれば揃うのか一向に見当がつきません.
そこでとりあえずやみくもにトライしてみるとします.
この手法は言い換えると次のようになります.
アルゴリズムBZ:
入力: スクランブルされたキューブ
出力: 完成状態のキューブ
(Step 1) 回転させる面(6パターン)と角度(3パターン)をランダムに決定してキューブの面を回転させる.
(Step 2) キューブが完成したら終了,完成しない場合 Step 1 に戻る.
ソート対象の要素のスワップ(サイクリックなスワップ)と考えられますので,これはボゾソート(の派生)に対応します.
ボゾソートも乱数に基づくソートのアルゴリズムである。リストがソートされていなければ二つの要素をランダムに取り出して入れ替え、リストがソートされているかどうかを調べる。 ボゴソート – Wikipedia より
こちらも無限の猿の定理により十分長い時間をかければ完成することが示せます.
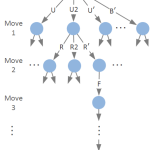
「ルービックキューブをアルゴリズムで解くということ」の記事で説明したように,ルービックキューブの取りうる任意の状態は『ルービックキューブの状態木』のあるノードに対応します.
ここで『ルービックキューブの状態木』とは完成状態をルートとしたときの20段の18分木です.よってノード数は $ N = 18^{21} – 1 $ 個です.
しかし,ルービックキューブの1つの状態は『ルービックキューブの状態木』の複数のノードに対応することがありえます.
例えば,完成状態から「U D」と操作したときの状態と「D U」と操作したときの状態は等しいです.
よって,$N$ をルービックキューブの完成状態から到達可能な状態数で割った値を,1つのルービックキューブの状態が『ルービックキューブの状態木』に割り当てられる個数とします.
ルービックキューブの状態木のノード数は $ N = 18^{21} – 1 $,
ルービックキューブの完成状態から到達可能な状態数は $ S = (8! \cdot 3^{8} \cdot 12! \cdot 2^{12}) / (2 \cdot 2 \cdot 3) = 43252003274489856000 $ であるから,
$ (18^{21} – 1) / S \approx 5305379 $
より,1つのルービックキューブの状態は平均でルービックキューブの状態木上の 5305379個 のノードに対応付けられると考えます.
さて,このアルゴリズムで何回の回転操作で完成状態に到達できるかですが,ランダムウォークになるので厳密なことは専門家でないのでよくわかりません.
ここでは,以下の文献を参考に,確率の逆数を平均的な試行回数として扱います.
参考文献: 必要試行回数とは:確率が結束して信頼性を得る回数について
完成するには完成状態の1操作手前の状態ノードにいる必要があるので,確率は $ 1 / 18^{21} \cdot 5305379 $ です.1回転操作をするたびに『ルービックキューブの状態木』でのノードを1つ遷移しますので,この確率の逆数を平均的な回転の試行回数 $T_{bz}$ と見積もって大丈夫そうです.
よって,
$ T_{bz} = 1 / ( 1 / 18^{21} \cdot 5305379 ) \approx 43251999884481279686 $
より,やみくもに 43251999884481279686回 ぐらい回転させればキューブは完成します.
1回転に1秒を要するとすると,仮定します.
すると,43251999884481279686秒です.これは 1371511919219年 すなわち 1兆3715億年です.
もし1秒間に10回転回せる(10tps)あの人ですら,この結果の桁が1個減るだけです.
1つ目のアルゴリズムでは,493兆7443億年ぐらいかかりましたので,ボゴソートと比べて完成するまでの時間は 500分の1ぐらい短縮しました.
しかし,これでも非現実的な時間です.やみくもにキューブを回してもキューブは完成しないのです.
まとめ
計算時間が爆発するといえば,おねえさん問題(動画1: YouTube)が有名ですが, 本記事ではコンピュータサイエンスの分野で時々ネタにされる,ボゴソート(動画2: YouTube)・ボゾソート・無限の猿定理(動画3: ニコニコ動画)とルービックキューブを絡めてまとめました.
動画1: 『フカシギの数え方』 おねえさんといっしょ! みんなで数えてみよう! – YouTube https://www.youtube.com/watch?v=Q4gTV4r0zRs
動画2: 15 Sorting Algorithms in 6 Minutes – YouTube https://www.youtube.com/watch?v=kPRA0W1kECg
動画3: 時間の比較 – ニコニコ動画:GINZA http://www.nicovideo.jp/watch/nm16202721
やみくもにキューブを回してもキューブは完成しないのです.賢く効率よく生きましょう.我々(コンピュータも含め)がルービックキューブを解くにはアルゴリズムが必要です.
下に示したのはtriboxさんによるルービックキューブのチュートリアルページです.わかりやすいので非常におすすめです.
最近,スマホ・タブレット用のページも完成したようですので,まだルービックキューブを揃えられない方はぜひこの機会に挑戦してみてはいかがでしょうか.
隠れた才能?
しかしながら最良計算時間はO(n)というクイックソートを超えるほぼ理論値であるため、今後量子コンピュータクラスの並列処理が可能になればクイックソートを抑えて脚光を浴びるとか浴びないとか言われている隠れた有望株でもある。 ボゴソートとは (ボゴソートとは) [単語記事] – ニコニコ大百科 より
そうなの?
謝辞
今回の計算には Wolfram|Alpha: Computational Knowledge Engine を使用しました.32bit / 64bit に収まってなくても正しく計算してくれるのでめちゃ便利です.
次回やるかも
Sarumawashi というルービックキューブを操作するC++ライブラリを以前作成してましたので,それを用いて「無駄な努力その2」の手法をシミュレーションしてみます.
ちなみに,Sarumawashi は無限の猿定理からその名前の由来を得ています.







![WCAデータベースたわむれ入門 [Speedcubing Advent Calendar 2014]](https://www.terabo.net/wordpress/wp-content/uploads/from-hawaii-150x150.jpg)