 terabo.net
terabo.net 人生ラボラボ
N×N×Nキューブを目隠しで解くときの記憶量考察
あけましておめでとうございます. 2015年最初の記事です.
Contents
概要
本記事では,N×N×N (2×2×2 ~ 7×7×7) キューブを目隠しで揃えるための記憶量を計算し比較考察する. キューブの記憶量に関する問題はSNS等でたまに話題になるが,この際ちゃんと定式化してみた.
現在の N×N×N キューブ目隠し解法の主流はコーナー,エッジ,センターそれぞれの3点交換(3-cycle)であり,記憶方法もそれに即して facelets (ステッカー)列を記憶する方法である. 本記事もその方法でキューブの状態を記憶する.
初めに断っておく. 同じサイズのキューブでも記憶方法の違いやキューブの状態によって記憶量が少々異なる. 本記事では,異なるサイズのキューブ間での記憶量を比較するのが目的であり各サイズのキューブにおいて厳密に記憶量を計算することはしない.概算である.
いきなり結果を示す
いきなりだが結果を示す.以下の表に,2×2×2 から 7×7×7 を目隠しで解くときのキューブ状態の記憶量を示す.
具体的な算出方法は本記事の後半に記述したので,興味のある方はそちらを参照されたい.
| キューブの種類 | 記憶量 |
|---|---|
| 2×2×2 | 31 bit |
| 3×3×3 | 80 bit |
| 4×4×4 | 239 bit |
| 5×5×5 | 392 bit |
| 6×6×6 | 655 bit |
| 7×7×7 | 912 bit |
以下の表は,2×2×2 から 7×7×7 までのそれぞれを正規化したときの数値である.
例えば,5×5×5 のキューブ状態を記憶するには 3×3×3 の4.9倍の記憶量が必要であることを表している.
| 2×2×2 | 3×3×3 | 4×4×4 | 5×5×5 | 6×6×6 | 7×7×7 | |
|---|---|---|---|---|---|---|
| 2×2×2 | 1 | 2.60 | 7.77 | 12.8 | 21.3 | 29.7 |
| 3×3×3 | 0.385 | 1 | 2.99 | 4.91 | 8.21 | 11.4 |
| 4×4×4 | 0.129 | 0.334 | 1 | 1.64 | 2.74 | 3.82 |
| 5×5×5 | 0.0784 | 0.204 | 0.609 | 1 | 1.67 | 2.33 |
| 6×6×6 | 0.0469 | 0.122 | 0.365 | 0.598 | 1 | 1.39 |
| 7×7×7 | 0.0337 | 0.0875 | 0.262 | 0.430 | 0.718 | 1 |
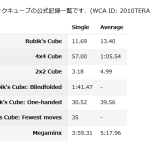
2014年末に Marcin Maskow Kowalczyk 氏がYouTubeに投稿した,Multiple-blindfolded 150個挑戦(125個成功)が記憶に新しい.
3×3×3 キューブ150個の記憶量は 11970bit (= 1496byte = 1.46KB) であり,2×2×2 だと約389個分,5×5×5 だと約30個分に相当する.
Mike Hughey 氏は過去に,2×2×2 から 7×7×7 までをリレー式に一気に記憶して揃えるという挑戦を試みている.
このときの記憶量は 2308bit (= 289byte) であり,3×3×3 に換算すると約29個分である.
最近話題の,13×13×13 を目隠しで解くときのキューブ状態記憶量は 3721bit であり,これは 3×3×3 だと約47個分に相当する.
以下は,情報理論の情報量に基づく計算方法である. 興味のある方はご覧になられたい.
計算の準備
まず,記憶量を定義する.
記憶量(情報量)は次のように定義される.
パターン数が $ p $ のものを $ n $ 個記憶するときの記憶量 $I$ は
$ I = n \log_{2} p \:\: — (*) $
である.
ここで対数の底はなんでも良いが,ここでは2にして記憶量の単位をbitとする.
これは,例えば状態数が8であるものは 3 bit で記憶することができる,ということを言っている.
次に,各 facelet を分類する.
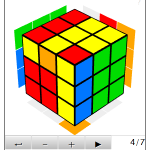
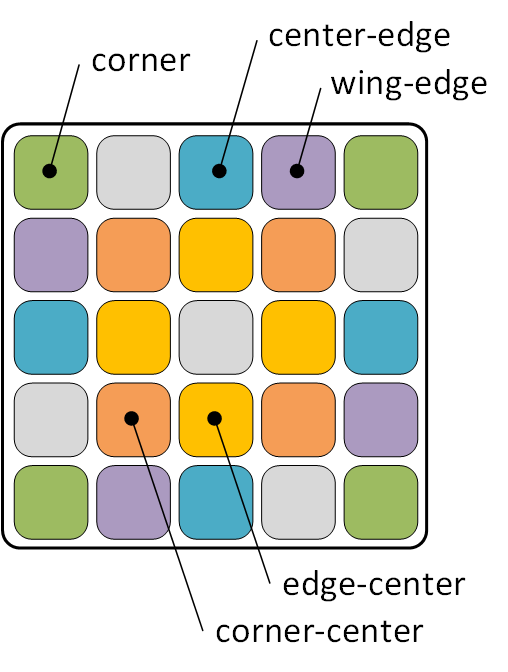
図は,5×5×5 の一面を表している.慣習に従い次のような名称で呼ぶ.グレー色で表した部分は fixed か他が揃えば勝手に揃う部分なので考えなくて良い.
コーナーは corner,エッジは center-edge と wing-edge,センターは edge-center と corner-center である.本記事ではこのように分類されたものを sub-problem と呼ぶことにする.
2×2×2 は,corner のみの sub-problem で構成される.
3×3×3 は,corner と center-edge の sub-problems で構成される.
4×4×4 は,corner と wing-edge と corner-center の sub-problems で構成される.
5×5×5 は図の通り.
N×N×N (ただしNは2以上かつ偶数) は,corner といくつかの wing-edge といくつかの corner-center の sub-problems で構成される.
N×N×N (ただしNは3以上かつ奇数) は,corner と center-edge といくつかの wing-edge といくつかの corner-center といくつかの edge-center の sub-problems で構成される.
各 sub-problem は互いに独立であり,これらは独立して解かれる.例外はパリティ処理である.ただし記憶はそれぞれ独立に完結する.
各 sub-problem は1面あたり4個で6面の計24個の facelets で構成される.記憶時はバッファを除く23個の facelets に記憶用の記号が割り当てられ,区別される.ただし,corner と center-edge では同じ cubie (物理的に分解したときの1パーツ) に複数の記号が割り当てられるため,バッファと同じ cubie に割り当てられる全ての記号は不必要である.よって corner と center-edge の区別はそれぞれ21と22である.
各 sub-problem の記憶時 facelets 記号列 (今後,記憶記号列と呼ぶ) の長さは,キューブ状態により異なる.
Sub-problem 内の全ての facelets が本来自身の存在すべき位置に存在しなく複数ループが発生しないとき (これを標準状態と呼ぶことにする),記号列の長さはその sub-problem の (cubieの数 – 1) である.1を減ずるのはバッファ分である.すなわち,corner の記憶記号列の長さは7,center-edge の記憶記号列の長さは11,その他の記憶記号列の長さは23である.
ただし,この長さはすでに揃っている cubie が存在するときこれより短くなるし,ループが複数個になるときや flip/pivot が存在するときこれよりも長くなる.ループ時に途切れる最後の記号を記憶しないため記憶記号列の長さが増加しない方法を用いる競技者もいるが,それは明示的に記憶しないだけで暗示的にループすることを記憶するためどちらも同じである.
厳密に計算するのであれば,キューブの取り得る全状態を考え,それぞれの確率にそのときの記憶記号列の長さを掛けて総和をとるべきである (情報量エントロピー/期待値の考え方).しかし,前述の要因により長さは増減するものの大まかに上で述べた標準状態とそんなに違うことはないと仮定し,標準状態での記憶記号列の長さを用いることで近似する.これは実際の競技者の感覚として違和感を感じる値ではなく現実的であると考える.
ただし,センターに関しては cubie に1色しか割り当てられないため,コーナーやエッジと比較してスクランブル時にすでに正しいポジションに配置されている可能性が高く,今回の方法は若干悲観的な見積りである.これの改善は今後の検討事項とする.
以上の数値をまとめたのが次の表である.
| Sub-problem | 記憶記号数 | 記憶記号列の長さ (標準状態) |
|---|---|---|
| corner | 21 | 7 |
| center-edge | 22 | 11 |
| wing-edge | 23 | 23 |
| edge-center / corner-center | 23 | 23 |
計算するよ
以上の議論をもとに,各サイズのキューブの目隠し解法用キューブ状態の記憶量を計算する.
3×3×3
3×3×3 は corner と center-edge の sub-problems に分けられる.
それぞれの標準状態での記憶記号列の記憶量(情報量)は,式(*)より求めることができる.キューブ全体の記憶量は情報量の加法性により,各 sub-problem の記憶量の総和で計算できる.
よって,3×3×3 のキューブ状態記憶量 $ I_3 $ は次のように計算できる.
$ I_3 = 7 \cdot \log_{2} 21 + 11 \cdot \log_{2} 22 \approx 80 {\rm [bit].} $
2×2×2
2×2×2 は corner のみの sub-problem である.
よって,2×2×2 のキューブ状態記憶量 $ I_2 $ は次のように計算できる.
$ I_2 = 7 \cdot \log_{2} 21 \approx 31 {\rm [bit].} $
4×4×4
4×4×4 は corner と wing-edge と corner-center である.
よって,4×4×4 のキューブ状態記憶量 $ I_4 $ は次のように計算できる.
$ I_4 = 7 \cdot \log_{2} 21 + 23 \cdot \log_{2} 23 + 23 \cdot \log_{2} 23 \approx 239 {\rm [bit].} $
5×5×5
5×5×5 は corner,wing-edge,center-edge,corner-center,edge-center で構成される.
よって,5×5×5 のキューブ状態記憶量 $ I_5 $ は次のように計算できる.
$ I_5 = 7 \cdot \log_{2} 21 + 23 \cdot \log_{2} 23 + 23 \cdot \log_{2} 23 \approx 392 {\rm [bit].} $
6×6×6 以上 (一般化)
これ以上は,N×N×N として一般化する.
N×N×N (Nは2以上かつ偶数)
N×N×N (Nは2以上かつ偶数) の場合,sub-problem の個数は,
corner は1個,
center-edge は,0個,
wing-edge は,N列の内最も外側を除いた列の数の半分すなわち (N-2)/2 個,
edge-center は,0個,
corner-center は,wing-edge の内側に存在するので,wing-edge の個数の2乗で (N-2)^2/4 個である.
よって,N×N×N (Nは2以上かつ偶数) のキューブ状態記憶量 $ I_{Ne} $ は次のように表される.
$ I_{Ne} = 7 \cdot \log_{2} 21 + \frac{N-2}{2} \cdot 23 \cdot \log_{2} 23 + \frac{(N-2)^2}{4} \cdot 23 \cdot \log_{2} 23 {\rm [bit].} $
例として,$ I_6 $ は次のように計算できる.
$ I_6 = 7 \cdot \log_{2} 21 + 2 \cdot 23 \cdot \log_{2} 23 + 4 \cdot 23 \cdot \log_{2} 23 \approx 655 {\rm [bit].} $
N×N×N (Nは3以上かつ奇数)
N×N×N (Nは3以上かつ奇数) の場合,sub-problem の個数は,
corner は1個,
center-edge は,1個,
wing-edge は,N列の内最も外側と中央の列を除いた列の数の半分すなわち (N-3)/2 個,
edge-center は,wing-edge の個数と等しいため (N-3)/2 個,
corner-center は,wing-edge の内側に存在するので,wing-edge の個数の2乗で (N-3)^2/4 個である.
よって,N×N×N (Nは3以上かつ奇数) のキューブ状態記憶量 $ I_{No} $ は次のように表される.
$ I_{No} = 7 \cdot \log_{2} 21 + 11 \cdot \log_{2} 22 + \frac{N-3}{2} \cdot 23 \cdot \log_{2} 23 + \frac{N-3}{2} \cdot 23 \cdot \log_{2} 23 + \frac{(N-3)^2}{4} \cdot 23 \cdot \log_{2} 23 {\rm [bit].} $
例として,$ I_7 $ は次のように計算できる.
$ I_7 = 7 \cdot \log_{2} 21 + 2 \cdot 23 \cdot \log_{2} 23 + 4 \cdot 23 \cdot \log_{2} 23 \approx 912 {\rm [bit].} $
以上です.
今後の課題は,Megaminx,Pyraminx,Square-1,Skewb,Clock の記憶量を計算することです.
ご指摘,ご意見等ありましたら,コメントください.





![WCAデータベースたわむれ入門 [Speedcubing Advent Calendar 2014]](https://www.terabo.net/wordpress/wp-content/uploads/from-hawaii-150x150.jpg)