 terabo.net
terabo.net 人生ラボラボ
ルービックキューブをアルゴリズムで解くということ
ルービックキューブを解くアルゴリズムについて書きます.この記事では具体的なアルゴリズムの話はありません.
(情報工学的アプローチでの見方です.ルービックキューブを解くアルゴリズムは「群論」とも深く関わりがありますが,私は情報工学系の人間なので群論は全くわかりません.)
※ この記事はルービックキューブを解くアルゴリズムの概念的なものを説明した記事です. 実際のルービックキューブを我々人間が解くやり方は以下のページをおすすめします.とてもわかりやすく書かれています.
ルービックキューブの解き方はじめに
まず,いくら時間をかけて良いという環境のもとであればルービックキューブを単に解くということは実は非常に簡単なタスクです.
ただ,それをいかに効率良く解くか,というのが非常に重要なことで,多くの人々の興味の対象でもあります.
その手順がアルゴリズムです.
本記事ではルービックキューブを解くアルゴリズムの概念を説明した後,既存手法を 1)人間的アプローチ,2)コンピュータ的アプローチのそれぞれでごくごく簡単に分析し,自分がこれから試してみたいことをまとめます.
準備
3x3x3のルービックキューブを考えます.各コーナーキューブとエッジキューブの位置と向きによってキューブの”状態”を定義します.
例えば,完成されたキューブやチェッカーキューブやスーパーフリップは1つの状態です.
ちなみに,3x3x3のルービックキューブの状態数は43,252,003,274,489,856,000であることが知られています.
– Source: ルービックキューブ – Wikipedia
いま,あるキューブの状態を考え,この状態を$S_0$とします.
この状態$S_0$から全ての回転方法,すなわち6面に対する時計回り・反時計回り・半回転,合計18通りを試すと新しい状態$S_1^{m_1}$へ遷移します.
さらにその新しい状態からそれぞれ全回転を試すと,それぞれの状態から新しい18通りの状態$S_2^{m_2}$が生成されます.
これを繰り返します.
下にこの操作を図示したものを示します.
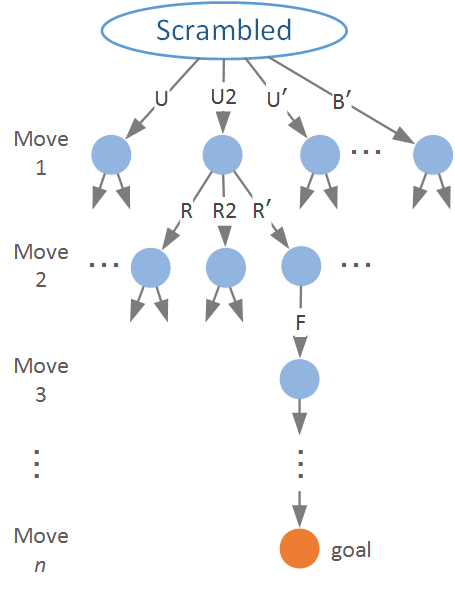
図中の”Scrambled”はスクランブルされたキューブの状態を表し,ルートノードとします.
ルートノードから回転を全通り試して新しいキューブ状態を展開していきます.
数が多すぎて全てを描ききることはできませんが,だいたい図のようになります.
これは,データ構造で言うところの「木構造」です.18分木です.これをここでは探索木と呼ぶことにします.
(例えば,ある状態からU面90度回転を4回繰り返せば同じ状態に戻りますが,それによってグラフを循環させることはせずに次々と新しいノードを展開していくとします.)
ちなみにこの木のことをコンピュータサイエンス(ゲーム理論)の用語で「ゲーム木/ゲームツリー」といいます.
コンピュータ将棋やチェスなどでは必ずと言っていいほど使用されます.
ここで,「ルービックキューブの任意の状態から高々20手の回転操作で完成状態に戻すことができる」という定理があります.
20は”God’s Number”と呼ばれています.
– Source: God’s Number is 20
ちなみに,ここでは直接関係しませんが,スーパーフリップと呼ばれる状態から完成手順に戻す操作の下限値も20手であることが示されていますので,この数字が覆ることはありません.
この定理より,先ほどの探索木において,深さ20(すなわち20手)までノードを展開すると,必ず完成手順にたどり着くことがわかります.
ナイーブに解くだけなら簡単なタスクをであるというのはこの意味です.
ただし,とても時間がかかります.
深さ20段の18分木は,何個のノードで構成されるでしょうか.$18^{20}+1$個でしょうか.
1個あたり1ms要するとして,計算に何秒必要でしょうか.面倒なので計算しません.
組合せ爆発です.お姉さんの問題です.
そこでアルゴリズムを利用します.
アルゴリズムの概念
まず,これだけ大きい探索空間をいきなり彷徨う前にやるべきことがあります.
もっとも有効に働くのは「問題をサブ問題に分割する」ということでしょう.
これはどういうことか,図で説明します.
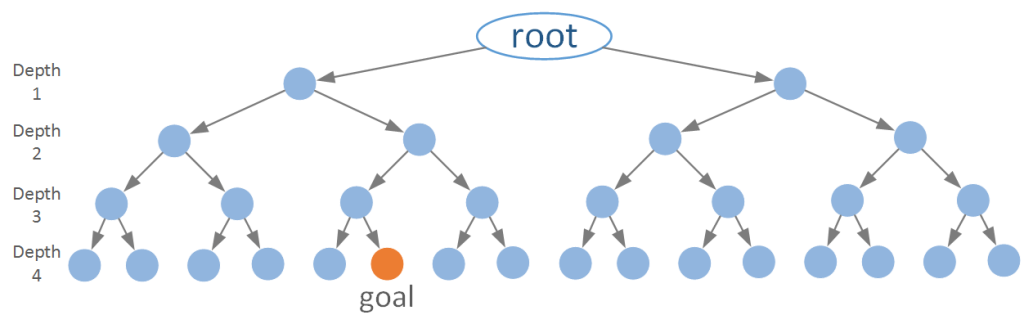
上の図は,簡単な探索木を描いた図です.
深さ4の2分木です.
スタートノードとゴールノードが設定されています.
この例の場合,大したことないノード数なので容易にゴールに到達しそうな感じがしますが,20段の18分木ではそう簡単にいきません.
そこで,下の図のように「サブゴール」を設定します.
そして,「スタートノードからサブゴールまでを探索する問題」と「サブゴールからゴールノードまで探索する問題」の2つの問題に分割します.
もちろん2分割に限らず,もっと多くのサブ問題に分割することも可能です.
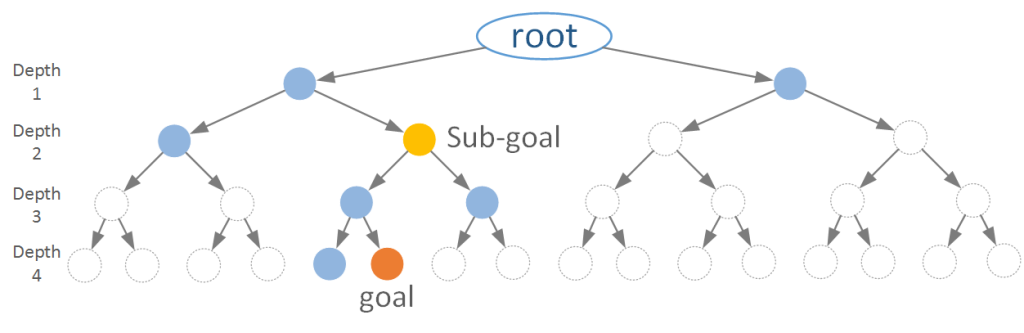
図からわかるように,展開するノードがかなり少なくなっています.
適切にサブ問題に分割することが,効率良く解くことの近道です.
本記事では,サブ問題を”phase”とも呼ぶことにします.
重要なポイントはサブ問題をどのように設定するかです.
ルービックキューブの探索木でのサブ問題の設定には,次のような規則を定めると良いです.
- サブ問題は,そのサブ問題の上流にあるサブ問題で生成される状態を崩してはならない
- サブ問題でのノード展開方法に制限を設ける
以下に,実際のアルゴリズムを人間的なものとコンピュータ的なものの両方を取り上げて詳しく説明します.
人間的アプローチ
今まで,アルゴリズムという概念からコンピュータが解く風な書き方をしていましたが,実はこれは我々がよく知ってるCFOPなどの人間的解法にも当てはまります.
例えば,CFOPはその名の通り,Cross,F2L,OLL,PLLの4つのphase(サブ問題)に分割されます.
崩された状態からCross手順によりクロスが揃います.完成状態に一歩近づきます.
次のphase,F2Lに移ります.F2Lでは2層が揃いますが,この時前のphaseであるクロスが崩れていないこととF2Lの限定された手順を使用している点がポイントです.
同様に,OLLとPLLのphaseもそれぞれ前のphaseの完成状態を崩していなく,OLL手順やPLL手順といった限定された手順を使用している点がポイントです.
このように,サブ問題の設定によって完成状態にどんどん絞り込んで効率の良く解いていきます.
人間が解く方法なので,わかりやすいですが,コンピュータで解く場合も同じです.
コンピュータ的アプローチ
ルービックキューブの探索木を解く方法として,Thistlethwaite’s algorithm,Kociemba’s Algorithm(Two-phaseアルゴリズムとしても知られている), Korf’s algorithm が代表的なものとして挙げられます.
例えば,Kociemba’sアルゴリズムは2つのサブ問題に分割します.
- 崩された状態から全回転操作を用いて,ゴールは完成状態から”U,Dの時計回り・反時計回り・半回転とR,L,F,Bの半回転”で到達可能な状態
- 1つ目のサブ問題のゴールから”U,Dの時計回り・反時計回り・半回転とR,L,F,Bの半回転”を用いて,ゴールは完成状態
各サブ問題では,CFOPのように決まった手順を実行するのではありません.
より小さくなった探索木を探索アルゴリズムで探索します.
探索木を用いた探索で思いつくものとして,DFS(深さ優先探索),BFS(幅優先探索),IDDFS(反復深化深さ優先探索),ダイクストラ法,A*アルゴリズムなどでしょう.
ざっと調べた感じ,IDA*アルゴリズムがコンピュータでルービックキューブを解くアルゴリズムとして主流なようです.
確かに,探索空間がこれだけ広く,ゴールまで深さも不定であるため,A*のコスト関数をうまく設定できれば有効な手段だと思います.
多くのtwo-phaseアルゴリズムの実装では,IDA*サーチをベースにして,ルックアップテーブルを用いてさらなる高速化をしています.
しかし,実はサブ問題に分割しちゃえば,あとはめちゃくちゃ適当でも案外それなりに現実的な時間で解けてしまいます.
Thistlethwaite’s algorithmのサブ問題分割で,各サブ問題はA*探索ですがコスト関数が適当なのでほぼ全探索のような実装をgithub上にアップしていますが,だいたいどんな状態でも普通のラップトップPCで1分もあれば解けると思います.
現実的な時間ですが,実用的な時間ではありませんね.
Two-phaseアルゴリズムは有名で,大会公式のスクランブラやほとんどのタイマーアプリで実装されています.
私が昔作ったスクランブラのWebアプリChampler!もtwo-phaseアルゴリズムを使用しています.
Github上にはこのアルゴリズムを高速に実装したもの,例えばmin2phase,も公開されており,相当実用的なアルゴリズムです.
他にも,進化的アルゴリズム(遺伝的アルゴリズム)を用いた研究が近年でもされていて,厳密に理詰めで解く以外の方法も何かしらの優位性も見い出せるのではないかと思います.
– Reference(pdf): An Evolutionary Approach for Solving the Rubik’s Cube Incorporating Exact Methods
今後やりたいこと
と,ここまでルービックキューブをアルゴリズムで解くという概念と既存手法を簡単に紹介してみました.
3x3x3に限っては探索木の深さが20に限定されてしまっているし,他のNP問題と比べたらかなり簡単な部類に入ると思います.
実際,厳密的に解くtwo-phaseアルゴリズムで相当実用的です.
前章で説明したように,コンピュータでルービックキューブを解くアルゴリズムは様々なものが提案されています.
ルービックキューブは「パズル」であることを忘れてはいけません.ある意味「人間の直感」を大切にするとなにか良いことが起きるかもしれないし,無駄な探索が減るかもしれません.
メタヒューリスティクスな視野からルービックキューブを解くということに挑戦してみたいと思います.
これらの研究は今のところ私の知る限りほとんど報告されていません.
例えば,遺伝的アルゴリズム,SA法,タブーサーチ,蟻コロニー最適化,ニューラルネットワークなどです.
うまく働くかわかりませんが…
ちなみに,他に理詰めなアプローチとして,例えば,さっきのお姉さんの問題,この動画内では詳しく述べれていませんが,BDD/ZDDを用いて効率の良く解くことができます.
– 参考: ZDD入門-お姉さんを救う方法
あとは,ILPとかSATとかに帰着させるとか.できるかわからないけど.
これらが価値のある研究になるかはわかりませんが,暇な時に試してみたいと思います.
人間の直感×コンピュータ=最強アルゴリズム